BLOG

Read through! This is not a boring lecture. On the contrary, it may be the most valuable
application of algebra and geometry ever to exist. Mathematics is supposed to help us
understand the world and solve problems. And for you and us, the world revolves
around pizza. After reading this enlightening article, you will be the wisest person
among your friends and relatives. People will entrust you with the responsibility of
placing every order with your pizza delivery Detroit. You will become a pizza deity, and
the original house of pizza menu will have a pie named after you. What a way to
transcend into the history of humankind! Grab your calculator and keep reading.
Math for ordering pizza
The first problem to solve comes at the time of ordering: how many pizzas should we
get? The answer is in the pi within the pie. When your teacher told you that the area of
a circumference is found by squaring the radius and multiplying it by pi, you may have
wondered what use that could have in your life. Today, we are giving meaning to your
entire school time: this very formula helps you stand for the fact that you should always
go large. Math tells us that a large pizza contains four times as much pie as a single
medium one. This is twice as much as two mediums. Since a large never costs twice as
much, it is definitely the most cost effective choice.
Math also tells us that we would need four New York style pizzas to match a Chicago
deep dish pizza of the same diameter to have the same amount of food. You can pile up
the thin pizzas to get an equal volume than the thick one. But if a large New York style
pizza is twice as wide as a small Chicago pie, then they would both be the same
quantity.
Math for cutting pizza
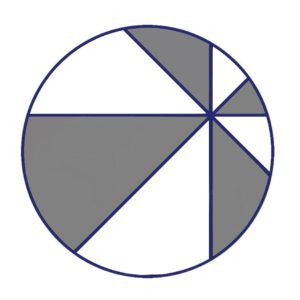
One of the most favorite theorems in math, possibly because it involves this popular
dish, is called the Pizza Theorem. This theorem arose from the need to maximize the
number of cut slices, a problem as relevant in math as it is in life. It is named after pizza
because it mimics its traditional slicing technique. Its basic principle states that if a
circular pizza is divided into multiple slices by making cuts at equal angles from an
arbitrary point, the sums of the areas of alternate slices are equal. This means that if
two people share a pizza sliced in this way by taking alternating slices, they both will get
an equal amount of pizza. Next time, you could try cutting your pizza like this and see
what happens:

The theorem shows that the sum of the white slices equals the sum of the gray ones.
Furthermore, if the pizza has one or more toppings, each covering a circular region
even if it is not concentric, and each cut crosses every region, then every person will
receive equal shares of toppings and crust.
Math for eating pizza
We do not wish to start an argument regarding a proper way of eating pizza. But if you
are one of those who use cutlery, it may be because you are not familiar with Carl
Friedrich Gauss's Theorema Egregium. This theorem, which translates from the Latin
meaning ‘remarkable theorem’, solves the problem of floppy slices dangling limply from
your hand because of the excess of toppings. The Gaussian curvature is a very abstract
concept which applies to very common things. For example, it links to the impossibility
of accurately depicting a world map on paper because of a distortion that occurs when
flattening a sphere. In the same way, flat things always retain a trace of their original
flatness when you try to give them volume, like a sheet of paper which is unavoidably
crinkled when you wrap a round object.
A pizza slice on a plate is flat. In order to eat it without the toppings falling off, you must
keep one direction of the slice in its original flat state. Fold the pizza slice sideways,
forcing it to become stiff in the direction that points towards your mouth. This natural
curvature is also found in the pizza box. The wrinkles in corrugated cardboard, apart
from providing aeration, keep the material thin and lightweight yet stiff enough to resist
bending.
Now that you have been educated in the most essential aspects of mathematics, visit
Paul’s Pizza or order our pizza delivery Detroit to put these theories into practice.